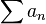Una serie ∑an se dice que es convergente (o que converge) si la sucesión SN de sumas parciales tiene un límite finito. Si el límite de SN es infinito o no existe, se dice que la serie diverge. Cuando este límite existe, se le llama suma de la serie.
Si todos los an son cero para n suficientemente grande, la serie se puede identificar con una suma finita. El estudio de la convergencia de series, se centra en las propiedades de las series infinitas que incluyen infinitos términos no nulos. Por ejemplo, el número periódico
tiene como representación decimal, la serie
 .
.
Dado que estas series siempre convergen en los números reales (ver: espacio completo), no hay diferencia entre este tipo de series y los números decimales que representan. Por ejemplo, 0.111… y 1/9; o bien 1=0,9999...
Sumas parciales
La sucesión de sumas parciales 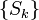 asociada a una sucesión
asociada a una sucesión 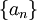 está definida para cada
está definida para cada  como la suma de la sucesión
como la suma de la sucesión 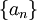 desde
desde  hasta
hasta  :
:
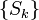 asociada a una sucesión
asociada a una sucesión 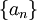 está definida para cada
está definida para cada  como la suma de la sucesión
como la suma de la sucesión 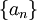 desde
desde  hasta
hasta  :
: .
.
Muchas de las propiedades generales de las series suelen enunciarse en términos de las sumas parciales asociadas.





 , donde an = bn − bn+1:
, donde an = bn − bn+1:

 , con
, con  =
=  .
.